나의 성장 방정식
삶의 거시적인 방향성을 찾아가는 몇달간의 과정동안, 나의 궁극적인 추구점이 무엇인지 가장 먼저 고민하게 되었다. 몇달간의 숙고를 통해 일차적으로 내렸던 결론은 “복리적인 성장”이었다. 다양한 사람들의 글을 읽으면서 유난히 복리라는 키워드가 반복된다고 느꼈고, 그래서 우선적으로 그 키워드를 빌려서 나의 성장을 작성해 보았었다.
초기 아이디어
올해 10월부터 친구와 함께 Life Interest 라는 뉴스레터를 작성 중이다. 이름에서 알 수 있듯, 복리적 삶을 위해 지녀야 할 다양한 관점과 태도에 대해서 다루는 뉴스레터이다. 이 뉴스레터의 첫 글로 원래는 복리적 성장에 대해 수식으로 서술하고자 했었는데, 너무 글이 길어져서 뉴스레터에는 담지 못했다. 이름에 “복리”가 들어가다 보니, 기본 복리 수식으로 포문을 열었다.
\[FV = PV \times (1 + r)^n\]여기서 $FV$는 미래 가치 (Future Value)를 의미한다. 그리고 이 값은 $PV$(Present Value: 현재 가치), $r$(이자율) 그리고 $n$(기간)으로 정의된다. 나는 이 수식을 다음과 같이 이해하고 있었다.
\[FV = PV \times (1 + Experience) ^ {Time}\]해석하자면, 많은 시간을 투입하고 많은 경험을 하면 성장할 것이라는 의미이다. 이를 2010년 경부터 인지하고 있었는데, 이때쯤 읽었던 말콤 글래드웰의 저서, 아웃라이어에서 주장하는 1만 시간의 법칙에서처럼, 어떤 것을 1만 시간동안 한다면 전문가가 될 수 있다고 주장했기 때문이다.
점차 느려지는 성장, 그리고 그 이유
하지만 오랜기간 다양한 경험을 하다 보니, 어느 순간 나의 성장이 다음과 같이 느려지고 있다는 걸 느낄 수 있었다.
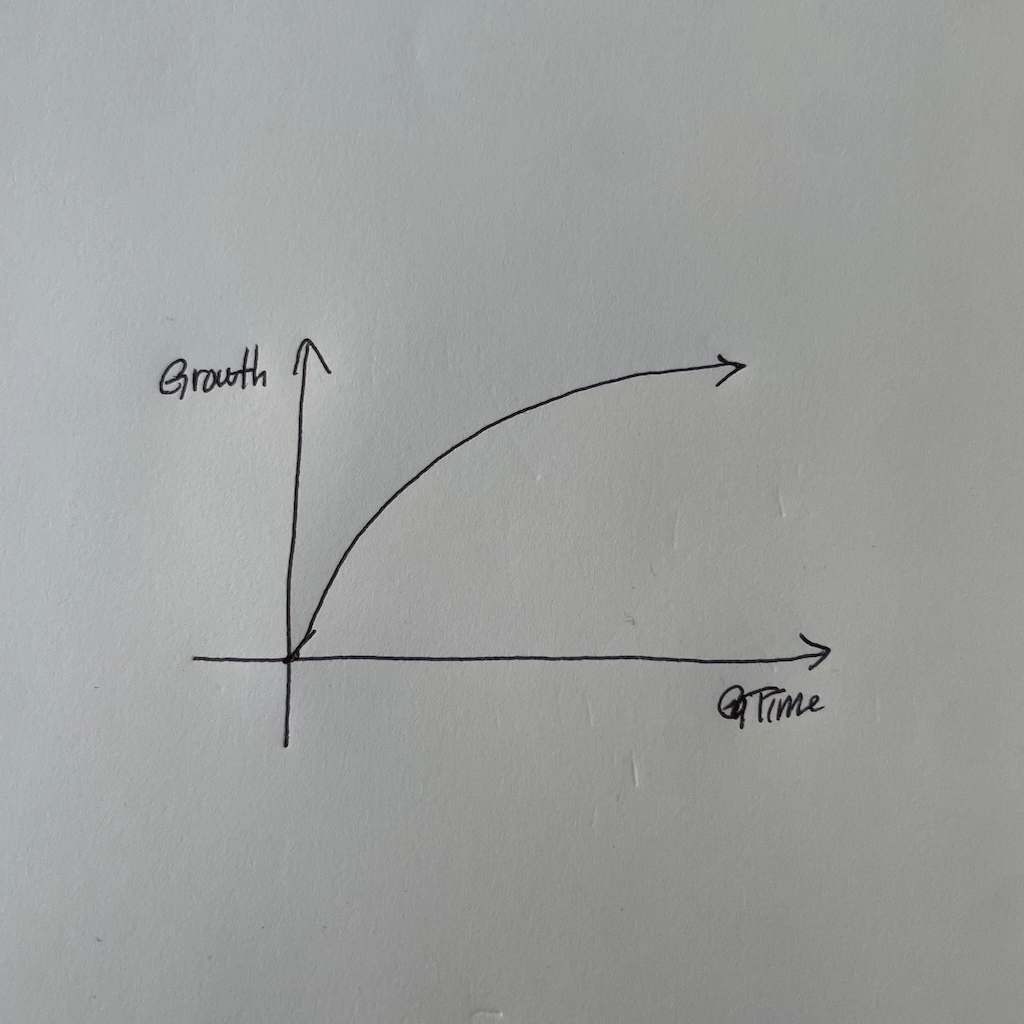
시간이 지남에 따라 아래와 같이 성장이 더뎌진다고 느껴졌다. 위 수식이 맞다면 지수적 성장을 해야 하겠지만 그 반대이므로, 위 수식이 아주 잘못되었다는 결론에 도달했다. 그래서 수식을 다음과 같이 바꾸었다.
\[FV = PV \times (1 + Density) ^ {Focusing\ Time}\]경험이 아니라 밀도로, 시간이 아니라 집중한 시간으로 요소가 바뀌었다. 약간 복잡해졌지만, 조금 더 구체적인 요소들을 반영할 수 있게 되었다. 저는 각각의 항목을 다음과 같이 정의할 수 있다고 본다.
\[Density = \frac{Number\ Of\ Meaningful\ Experiences}{Spent\ Time}\]밀도는 사용한 시간 대비 의미있는 경험을 얼마나 했는지에 대한 값으로 나타낼 수 있다. 같은 시간 내에 더 많은 의미있는 경험, 즉 아하 모먼트를 느낀다면 더 빠르게 성장할 수 있을 것이다.
그렇다면 $Focusing\ Time$항목을 보자. 왜 굳이 $Focusing$이 붙었을까? 나는 무언가 학습할 때, 극초기가 아닌 이상 단순히 시간을 많이 소비한다고 해서 그만큼 결과가 좋아진다고 생각하지 않는다. 특히 내가 속한 지식 노동군은 더더욱.
실제로 이를 연구한 안데르스 에릭손 박사에 의하면 1만 시간의 법칙에 대한 오해는 바로 여기서 온다고 했다. 단순히 시간을 많이 사용한다고 실력이 느는 것이 아니라, 의도적인 연습 과정을 통해서만 실력을 늘릴 수 있다는 뜻이다. 머리를 쥐어짜내서 무언가를 배우고 뒤트는 시간이 복리 연산에 도움이 될 거라고 믿는다. 그래서 focusing이라는 단어를 추가했다.
좀 더 실행하기 편하게
수식 자체로만 보면 군더더기 없이 깔끔하지만, 이걸 머리속에 넣어놓고 실행하기에는 너무 추상적이라 자꾸 실행이 제대로 되지 않는다고 느꼈다. 그래서 이 수식을 동일이 아니라 유사로 변경했다.
\[FV \approx PV \times (1 + Density) ^ {Focusing\ Time}\]그리고 각 항목들을 다음과 같이 대체할 수 있다고 보았다.
\[Focusing\ Time \approx Executions\times Retrospectives\] \[Density \approx \frac{Learning}{Time}\]집중 시간을 실행과 회고로
조금 극단적인 비유를 들어 보겠다. 체력을 다 쓸 정도로 온 신경을 다해 집중해서 햇반 하나의 밥알이 몇개인지 세어봤다고 하자. 집중 시간은 크지만 그게 나의 성장에 도움이 될까? 전혀 아닐 것이다.
무언가에 집중하는 것은 좋지만, 내가 왜 이 일을 하고 있는지 계속 인지하고, 더 잘하기 위해 어떤 선택들을 해야 하는지 계속 체크해야만 방향을 잃지 않고 더욱 의미있게 시간을 사용할 수 있다.실제로 전문가들은 일반인들과는 다르게, 작업하는 와중에도 “내가 원래 뭘 하려고 했지? 지금 이대로 가면 어떤 상황이 될 것 같지?” 와 같은 질문을 계속해서 던진다고 한다. 이를 Reflection In Action (행동 중 회고)라고 부른다.
\[Focusing\ Time \approx Executions\times Retrospectives\]이제 다시 이 수식으로 돌아와보자. 이 수식이 의미하는 바는 “일단 실행해아 하며, 그 실행에서 얻어가는게 있어야 한다”는 대전제를 의미한다. 다만 이 실행의 주기를 극단적으로 줄임으로써 더 지속적으로 나의 상황을 센싱하고, 새로운 정보를 파악하며, 원하는 목표를 달성하기 위해 실시간으로 상황을 조정 해 나가는 것을 의미한다.
나는 그래서 작업 시 30분에 한번씩 Reflection in Action을 수행하는 연습을 하고 있다. 크게 다음과 같은 질문 5가지를 간단하게 적어보면 RIA는 끝난다.
- 내가 지금 뭘 하고 있지?
- 원래 뭘 하려고 했지?
- 이렇게 계속 가면 어떻게 될까?
- 그걸 고려하면 지금은 어떤 옵션이 있지?
- 그중에 제일 먼저 어떤 일을 해 볼까?
밀도를 학습과 시간으로
각 잡고 앉아서 무언가를 배우는 것만이 학습이 아니다. 분명 효율적으로 학습하는 방법이 있고, 그 방법을 적용하면 할 수록 같은 시간에 더 많은 것을 배울 수 있으리라는 결론을 낼 수 있다. 즉 학습의 밀도는 아래와 같은 수식으로 파악할 수 있다.
\[Density \approx \frac{Learning}{Time}\]다만 이대로 두기는 아쉽다. 얼마전에 메모했던 글을 첨부해 본다.
시간 관리 > 에너지 관리로 관점을 옮기니 좀 더 맘이 편하고 유연하게 시간이 관리되는 느낌이다. 집중이 안되면, 시간 관리의 관점에서는 “아 빨랑 집중해야지” 하고 강제로 앉히는 느낌이라면, 에너지 관리는 “아 내가 지금 에너지가 조금 부족하구나. 조금 환기하고 와야지” 하는 식으로.
사실 우리는 더 무언가를 효율적으로 해야한다는 생각이 들면, “시간 관리를 잘 하자”라고 접근한다. 하지만 시간은 많은데 일을 하기 싫은 경우도, 실제로 하지 않는 경우도 많지 않은가? 그떄는 하려는 동기가 떨어졌던, 체력적으로 힘들건. 즉, 우리가 실제로 무언가를 하기 위해서는 에너지가 필요하다는 거다. 즉, 이렇게 변경해볼 수 있겠다.
\[Density \approx \frac{Learning}{Energy}\]뿐만 아니라, 전체 학습된 기억 중 장기기억이나 암묵기억으로 남는 비율이 높을수록 더 효율적으로 학습하는 것일 거다. 그래서 그 비율을 수식에 포함해보자.
\[Density \approx \frac{Learning}{Energy} \times \frac{Long\ Term\ Memory}{Total\ Learn}\]하지만 이렇게 했을 때 극단적으로 에너지를 줄이는 식으로 최적화를 할 지도 모른다. 이렇게 되면 학습 퀄리티가 낮아져서 전체적으로 손해를 보게 된다. 결국 Learning과 Energy는 사실상 비례 관계이다. 약간의 조정은 가능하더라도. 그렇기 때문에 전체 에너지의 총량을 곱해줘야 한다.
\[Energy \propto Learing\] \[Density \approx \frac{Learning}{Energy} \times \frac{Long\ Term\ Memory}{Total\ Learn} \times Energy^{total}\]결론
위에 나온 수식을 합치면 다음과 같다.
\[FV = PV \times (1 + Density) ^ {Focusing\ Time}\] \[Focusing\ Time = Executions\times Retrospectives\] \[Density = \frac{Learning}{Energy} \times \frac{Long\ Term\ Memory}{Total\ Learn} \times Energy^{total}\] \[(Energy \propto Learing)\]즉 지속적으로 실행하고 회고하며, 학습 자체의 효율을 늘리고 (적은 에너지로 많이 배우며) 전체 에너지의 총량을 늘릴수록 도움이 된다는 결론에 다다를 수 있다. 아마 몇달, 몇년간 지속적으로 수정해 나갈 계획이지만, 2024년 11월에는 다음과 같다.
2024. 11. 23
